Bq#7 Unit V Concept 1-5

How do we derive the Difference Quotient?

Watch...

BQ#4 Unit T Concepts 1-3 Tangent & Cotangent graphs

Why is a “normal tangent graph uphill but a “normal” cotangent graph downhill?

The graphs for tangent and cotangent are in every single way bit for some reason they end up looking weird at the end. This is because of the way their asymptotes are formed. We know that tangent and cotangent are (+) in quadrants 1 & 3, and (-) 2 & 4. To understand this more, remember that to get an asymptote the trig ration must be undefined to have an undefined ratio you need to divide by zero.

For tangent, we know the ratio is Y/X so... to get an asymptote X must equal to zero. This means to will have asymptotes at pi/2 & 3pi/2. So the graph of tangent cannot touch these lines, but somehow it must be are in quadrants 1 & 3, and (-) 2 & 4. The only way to draw this is making it look like it is going “uphill”

Cotangent, we know the ratio is X/Y so… it will have asymptotes wherever cos=0 or y=0. This means the graph will have asymptotes at 0, pi, 2pi. The only way to graph this is how we did it above, giving it a “downhill” looking graph.

BQ #3: Unit T Concept 1-3

How Do The Graphs of Sine and Cosine Relate To Each of The Others?

2nd quadrant

1st caption

The graphs of sine and cosine relate to the others through their asymptotes. If you remember, we can think of a graph as an unraveled unit circle. If we think of it like this than sine and cosine can relate to the other functions through the quadrants. Another thing that will help us bring everything full circle are the trig identities. If you need reference to the graph on desmos you can click here courtesy of Mrs. Kirch

Tangent?

One thing that will aid the explanation of this is are the trig identities. Recall that tan= sin/cos if you take a look at the graph the green (sin) and red (cos) lines are positive because they are above the x axis. If we use this in the identity it means that is sin and cos are positive than tangent will be positive, as you can see this is true because the tangent graph is above the x axis. In the second picture, one of the graphs is positive one is negative giving it an overall negative, this is the reason why the tangent graph is below the x axis. These are some of the ways that the graphs relate.

Cotangent?

The explanation for  cotangent will be much more concise because it is based on the rules as tangent. For the exceptions that the identity is cos/sin and the asymptotes are shifted over. The asymptote will be at 0,pi, and 2pi. Also,  The graph of cotangent has its asymptotes based on sine.

Secant?

Secant relates to cosine because it has asymptotes based on cosine its asymptotes are where cos is equal to zero. This is because an asymptote is formed when secant is undefined, and the ratio for secant is R/X to get this to be undefined X=0.

Cosecant?

The asymptotes of cosecant are based on sine. It has asymptotes where sine equals zero because the ratio must be undefined. The ration so cosecant is R/Y to get an asymptote Y=0

BQ#5 - Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do?

From the picture above we see that sine and cosine are always divided by R wich means they will be divided by 1. This means that they cannot be undefined. Of your ratio isnt undefined then you wont have an asymptote. Other trig functions it is possible to have asymptotes because you can divide by 0. And, as we know dividing by zero equals undefined wich cause asymptotes in graphs.

BQ#2 - Unit T Concept 2

How do trig graphs relate to the Unit Circle?

a. The period for sine and cosine is 2pi because thats is howl long it takes for the    pattern to repeat. By pattern I mean for the positive and negative quadrant patterns. We know that a trig graph of sine is ++-- this means that the first to quadrants of the graph will be above the X axis and the othe will be under. Tangent /Cotangent however, will be pi because you only need one section for the pattern to repeat. The pattern for tangent/cotangent is +-+- however you only need +- because the pattern repeats  already.

b. Sine and cosine have restrictions because the unit curcle is only goes up to. 1, -1, 0. For the same reason sine and cosine can only equal >-1 & <1. To quote  Mrs. Kirch, " Sine and Cosine cannot bust through the restrictions."

Reflection# 1: Deriving trig identities

Reflection

1.What does it actually mean to verify a trig identity?

-to verfify and identity you should get both sides equal to the same trig function. You simplify the messy side and then when yiu get the same trig on that side it is verified

2.What tips and tricks have you found helpful?

- One tip that i found helpful is converting the trigs to sin / cosine. If you have tan and cot you can switch those to sin and cos. this really helped me because it gives me something to do and gets my brain working. This is much better then just starring at a problem for 10 minutes. Another truck that i use when I am stuck is to split fractions. Split fractions is easier for me to work with then a big fraction.

3.Explain your thought process and steps you take in verifying a trig identity.  Do not use a specific example, but speak in general terms of what you would do no matter what they give you.

- when ever i am having trouble the first thing i look for is sibstituting an identity. If you cant plug this in then converting to sin/cos helps. Other than this you might be able to find a GCF in the equation. As a last resort square both sides and the. Find extrannneous solutions.

SP#7: Unit Q Concept 2

This SP7 was made in collaboration with Sarah Ngo.  Please visit the other awesome posts on their blog by going here. www.sarahnperiod1.blogspot.com

I/D3: Unit Q - Pythagorean Identities

Inquiry activity Summary

1.      Where does sin^2x+cos^2x=1 come from to begin with?

a.       To explain this we need to think back and remember basic trig functions. We know that sin=y/r and cos=x/r. The unit circle gives us a value for r which is r=1. We also need to recall that the Pythagorean Theorem is a^2+b^2=c^2. Now we have everything we need to prove this. First we choose an ordered pair form the unit circle, like (1/2,3/2). We can now plug this in to (y/r) ^2+(x/r) ^2=1. The equation we should plug into our calculator is to (1/2)^2+ (3/2)^2=1. This shows how we can use the unit circle and the Pythagorean Theorem to get sin^2x+cos^2x=1.

2.      Show and explain how to derive the two remaining Pythagorean Identities from sin^2x+cos^2x=1

a.      Once you read this paragraph you will definatly realize how easy it is to derive the rest of the Pythagorean Identitites. First, you have your original identity: sin^2x+cos^2x=1 you will divide this by cos^2. Once you have done this your new identity will be 1+tan^2x=sec^2x. To get the next identity you dived the original by sin^2, you will get 1+cot^2=csc^2.

Inquiry Activity Reflection

1. The connection that I see between Units N,O, and P are trig functions, trig ratios, and pythagorean theorem.

2. If I had to describe trigonometry in 3 words, they would be challenging, a little frustrating and rewarding. 

WPP 13-14: Unit P Concepts 6-7: Application of the Law of Sines and the Law of Cosines

Please see my WPP13-14, made in collaboration with Sarah Ngo, by visiting their blog here.  Also be sure to check out the other awesome posts on their blog.

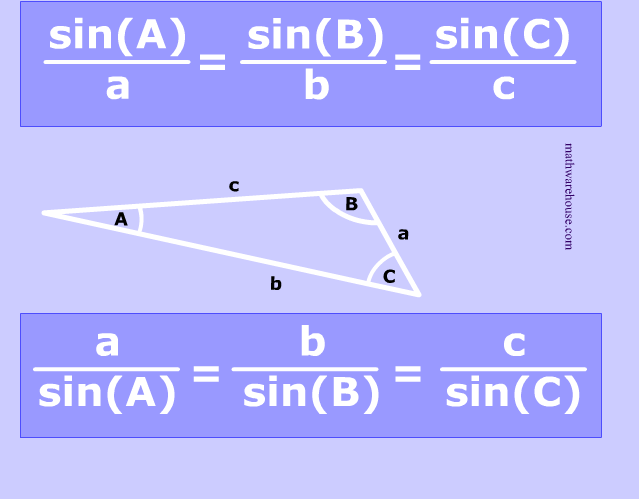
BQ#1 Unit P Concept 1 and 4: Law of Sines and Area Formula

    1.  Law of Sines

http://www.mathwarehouse.com/trigonometry/law-of-sines/images/formula-picture-law-of-sines2.png

Why do we need it?

• We need the law of sines because sometimes we are not dealing with right triangles. We don’t have the normal trig functions to solve non-right triangles. However, if we drop a perpendicular line h we can use the trig functions to help us solve the non-right triangles.

How is it derived?

• First, we cut the triangle in half. This reveals two right triangles within the non-right triangle. The law of sine’s are derived by taking the sine of angle A and angle C. we should end up with sinA= h/c & sinC= h/a Then we solve for h and simplify. This gives us c x sinA =h & a x sinC= h. If both equations are equal to h then they are both equal to each other. Now, to simplify this set a denominator of ac and cancel. You should end up with. SinA/a = SinC/c

2.   Area Formulas

• How is it related to the previously known formula? This formula is related to it because it is basically the same formula. The only difference is that we don’t know the value of h. to find the value of h we substitute (a x Sin C). In the next paragraph we will learn why and how we substitute this value.
• How is it derived?  The area formula is derived by finding the value of h. we know the are of a triangle is A= ½ bh. We know that SinC=h/a we solve for h, h= a x SinC. Plug this into the formula, A= ½ b( a x SinC ).

WPP #12: Unit O Concept 10- PICTURE

ANGLE OF ELEVATION

A man is on top of a mountain, the mountain is 200 feet tall the angle of depression is 35°. How far away ( laterally ) is he from the village at the bottom?

ANGLE OF DEPRESSION

The Los Angeles police department is preparing to invade a house. The angle of elevation is 45°, if the house is 50 feet away from the helicopter what is the distance that the officers have to drop from the helicopter to the ground?

I/D #2 Unit O- How Can We Derive the Patterns of Our Special Right Triangles?

INQUIRY ACTIVITY SUMMARY

          30 60 90 Triangles

·        The first thing you want to do is cut the equilateral triangle in half. To find the degrees we know that the bottom right corner is equal to 90, to bottom left corner is equal to 60 and the top since it was split in half is 30. After this, label the sides (a, b, c) from this we learn that a=1/2 b= unknown, and c=1. To find b we use the Pythagorean Theorem.

After this you should get b to equal (√3/2).now, we multiply everything by 2. The values should equal 1n, n√3, 2n. We use N because it is a variable, that shows that the ratio can be used in other multiples of the triangle.

45 45 90 Triangles

·        For this triangle we also start by cutting it in half diagonally. The angles are much easier to find in the triangle. Label all sides a, b, & c. we should find that a=1 and b=1.

 We plug these values in the Pythagorean Theorem and find that c=√2. We multiply all these values by “N” because it is a variable and it shows that this ratio works with all multiples of this triangle. Our final ratio should be a=n b=n & c=√2

INQUIRY ACTIVITY REFLECTION

·        Something I never noticed before about special right triangles is… you can derive the ratios for these triangles by setting the sides to 1 and using the square and the equilateral triangle.

·        Being able to derive these patterns myself aids in my learning because… when I forget the ratios I can still find them by using what I learned.

I/D #1: Unit N Concept 7: Deriving the Unit Circle Using Special Right Triangles

Inquiry Activity

In this activity we learned about the three special right triangles. We had to use online sources to figure out the rules for these triangles. We had to label the measurements of the triangles, assuming that the hypotenuse equaled 1.

1)  30 Degree Triangle

A thirty degree right triangle is called this because it consists of three angles that are 30, 60, and 90. The adjacent side is (x), opposite is (y) and the hypotenuse is (r). The adjacent value is √3x, the opposite is X, and the hypotenuse is 2x. We need to simply the three sides, and we are told that the hypotenuse must equal 1. We now know that the value of the hypotenuse (r) =1. To find the other sides we figure out what X is. X=1/2, this is the value of our opposite side (y). Now we need to find the value of (x), simplify (½) x (√3) = √3/2. We can plot these values as ordered pairs. X=√3/2, Y= ½. This correlates with the ordered pair of 30 degrees in a unit circle, as well as the coterminal angles.

2)   45 degree triangle

In a 45 degree triangle we have two angles with 45 degrees, and a right angle. The value of the sides are… adjacent side is (x) =X, opposite is (y) =X, and the hypotenuse is (r) = X√2. So we know that R = 1, but to find the rest we need to find X. We dived the other sides by X√2 and are left with 1/√2. However we can’t leave a radical in the denominator so after rationalizing we get X=√2/2. This correlates to the ordered pair in a UC because the coordinate for a 45 deg is (√2/2, √2/2).

3)   60 Degree Triangle

 The 60 degree triangle is basically a 30 degree angle but the adjacent side is (x) =X, opposite is (y) = X√3, and the hypotenuse is (r) = 2X. To get the hypotenuse to equal 1 you divide 2x by 2x. You also divide x√3 by 2x, and x/2x. In the end we get R=1, X=1/2, and Y=√3/2.

4)  How Does This Help Us Derive the Unit Circle?

This activity helps us derive the unit circle because we learn the reason why we have the coordinates in a unit circle. Looking at a unit circle, for a 45 degree angle we see the coordinates are (√2/2, √2/2). But, why are these the coordinates? These are the coordinates because this was the answer of what we calculated on a 45 degree triangle, X=√2/2 and Y=√2/2.

5) Quadrants

In this activity the triangle were all in quadrant I, the values change because ther signs become negative and positive. However if the 45 degree triangle was on quadrant II the x value would be negative. If the triangle was on quadrant III both x and y values would be negative. If the triangle was on quadrant IV then just the y value would be negative.

Inquiry Reflection Activity

1. The coolest thing I learned from this activity was the measurements of the sides of the triangles correlate to the coordinates of a unit circle.
2. This activity helped me in this unit because now I know that there is a reason for the coordinate, and if I don’t have a UC then I can just calculate it.
3. Something I never realized about special right triangles and the unit circle is in the unit circle there is many triangles that make up the coordinates.

RWA #1- Unit M Conceot 4-6: Parabola

1) Definition: The set of all points that are equidistant from the focus to the directrix.

y2 = 4ax

y2 = -4ax

x2 = 4ay

x2 = -4ay

To define a parabola it is important you look at its equation. As we can see above, in the first two example, when the y is squared, the graph goes to left and right. Having p positive or negative decided which direction it will go. For the other two equations algebraically, the x is squared and p also change signs. This transfer graphically because depending on the sign of p it will either open up or down.

 As we can see above, in the first two example, when the y is squared, the graph goes to left and right. Having p positive or negative decided which direction it will go. For the other two equations algebraically, the x is squared and p also change signs. This transfer graphically because depending on the sign of p it will either open up or down.

The key parts of the parabola are the directrix, p value, axis of symmetry, vertex, and focus. The axis of symmetry is a line that cuts in between the parabola, perpendicular to the axis of symmetry is the directrix. The focus is p, which is a point inside the parabola. The distance from p to a point in the graph should be the same from that point on the graph to the directrix. The p-value is also important because if p is less than one the graph will look skinny if it is greater than 1 it will become fatter.

Link to parabola explanation: ( http://youtu.be/-1MzoyzWxo4 )

<iframe width="420" height="315" src="//www.youtube.com/embed/-1MzoyzWxo4" frameborder="0" allowfullscreen></iframe>

3. Parabolas are everywhere, they are essentially a curved line. Kicking a soccer ball is a parabola. The vertex of the path of the soccer ball would be at the point where the soccerball is highest. One peal world event where parabolas are used are in the reflectors in your flash light. “rays emanating from the focus point will reflect off the parabola parallel to the axis of symmetry.” (http://youtu.be/Djnwlj6OG9k)

4. works cited

http://youtu.be/Djnwlj6OG9k( flashlight RWA)

http://www.mathsisfun.com/geometry/parabola.html (picture of parabola)

WPP 10: Probability of Independent, OR, and combinations

WPP #9: Unit L Concept 4-8 : Calculating Possibilities Using Different Methods